There’s something particularly satisfying about putting that last piece into a big puzzle. And nothing is more frustrating than the dreaded realization, as you are just about finished, that a piece is missing, and when the frantic search under chairs, tables, and couches ensues. Sure, the picture is mostly there and you can see whats going on, but there’s a gaping hole that screams for attention and demands to be filled. It’s bad enough if you simply knocked the piece off the table, or if it fell out of the box down in the basement, but what if you weren’t completely certain the piece ever existed in the first place?
In a sense, that’s where the particle physics community has been for the past few years. A beautiful picture had been constructed encompassing almost everything that had been observed over several decades worth of experiments, but it wasn’t finished. Everyone had a good idea of what belonged in that hole, but no one had actually found the piece that tied everything together. And that’s the significance of last week’s discovery of what looks to be the Higgs Boson: It’s the crowning achievement, the final step in a particular chapter of our understanding of nature. This is not to say, to be sure, that we now understand everything in particle physics, or that there’s nothing left to do, but it’s a monumental discovery and a confirmation of decades of work.
A question remains, though: How did physicists find what the beautiful picture looks like before actually finding the pieces that make it up? Modern physics seeks to describe the natural world based on mathematical laws—generally speaking, by observing the world around us and describing what is observed with mathematical formulas. At root, it is a response to the things around us. Why, then, is the physics community excited but not surprised by this new particle? Physicists are excited because the particle had never been observed before. But they aren’t surprised because, in a sense, they knew it had to be out there—it was needed to make a beautiful mathematical theory work.
Why should some nice mathematical theory be enough to convince us that a certain particle must be there? In one sense it is not enough, which is why the actual observation of the particle is so important to confirm the theories. But because physics has been so successful in using mathematics to describe physical phenomena, there is confidence that any new physics has to fall into some nice coherent theory. Now, someone could try to simply sit in a room and come up with the most beautiful mathematical theory imaginable, but there is no reason to think it has any actual connection to the real world. Thus, true science can never drift too far from observation. But the power of mathematical principles to guide our investigations and predict results is amazing. So many other things observed in particle physics fit into a particular framework—dubbed the Standard Model—that, while there are other possible explanations, none are quite as simple and neat. The Higgs Boson just had to be the right answer—and it looks like it really is.
Assuming this new particle really is the capstone to the Standard Model, there is much more for particle physicists to understand. How do we know this? Because although it is a remarkable mathematical description of a particular slice of nature, there are tantalizing signs that the the Standard Model is only a small piece of an even more beautiful, simple, and fundamental mathematical structure—though it is far from clear exactly what that structure is.
The amazing ability of mathematical laws to describe what often seems to be an ephemeral and unpredictable world, and the astounding ability of the human mind to probe and understand these laws of nature, are often taken for granted in the modern world. The impressive success of science and technology leads us to think naively that there is nothing they can’t describe. Yet, if they’re honest, physicists will admit that, for all the amazing things mathematical theories can describe, they have no explanation for why they should have such confidence in them at all. Further consideration should lead to the acknowledgement of what might truly exist that is beyond the explanatory power of numbers. There are philosophical truths wrapped up in these questions—which science is ultimately not able to answer—that are infinitely deeper than what is suggested by the irresponsible and unfounded popular name for the Higgs Boson, the “God particle.” Scientific investigation and mathematical laws, and the questions that follow on our relationship to nature, should lead us toward the God who has “arranged all things by measure and number and weight” (Ws 11:20).
✠
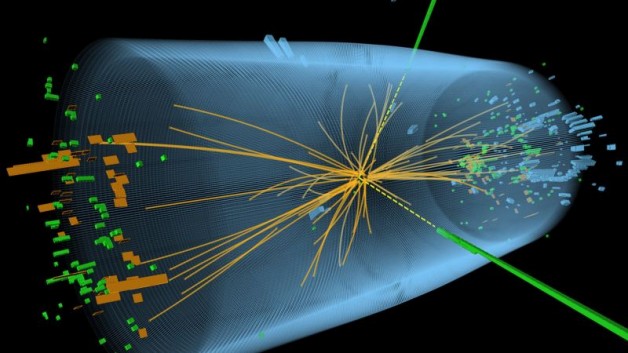
Image: an event recorder, using the CMS detector at CERN, with characteristics of the Higgs Boson